The scientific revolution of the 16th and 17th centuries is generally regarded as one of European civilisation’s greatest achievements. This revolution probably could not have occurred without groundwork laid by a somewhat earlier intellectual revolution, which was largely brought about through the work of a single individual. The role he played in this revolution was largely forgotten for several hundred years, very nearly lost to history entirely, and is still not widely known. The name of this individual? Leonardo!

No, not that Leonardo, of Vinci, but Leonardo of Pisa. “Leonardo of where?” I imagine most of you will be thinking, since this name is likely to be recognised only by scholars interested in the history of mathematics. Among mathematicians, Leonardo is better known under the name Leonardo Fibonacci or, more commonly, just Fibonacci, a title which was not conferred upon him until the 19th century.

Although Leonardo was one of the most distinguished mathematicians Europe managed to produce during the entire middle ages, very few details of his life are known. He was born some time around 1170 AD, but the exact year is not known. He became famous within his lifetime, and remained so for a couple of centuries after his death, but by the end of the 15th century, his achievements had largely been forgotten.

The extent of Leonardo’s lapse into obscurity is well illustrated by a wonderful anecdote told by Keith Devlin in his book, Finding Fibonacci, an account of his quest to learn more about Leonardo. Prof. Devlin was visiting Pisa in 2002, shortly after becoming interested in the life of Leonardo, and was attempting to visit some of the memorials to Leonardo which he had heard were to be found scattered around Pisa. One of these was a statue, on whose location Prof. Devlin’s sources had disagreed.

After a fruitless afternoon’s searching for the statue in the places that had been given as its purported location, Prof. Devlin finally resorted to enquiring at the local tourist information office, where the following exchange took place:

“Where is the statue of Leonardo of Pisa?”

“You mean Leonardo Da Vinci” – this uttered, not as a question, but with a tone of absolute confidence.

“No, Leonardo of Pisa.”

“Leonardo Da Vinci” – this being accompanied by a withering look typically reserved for the most irritatingly ignorant of foreign tourists.

“No, Leonardo of Pisa – Fibonacci, the mathematician.”

“There is no Leonardo of Pisa. No statue.”

After leaving the tourist information office, however, Prof. Devlin did eventually manage to find the sought-for statue – in the Camposanto, a monumental cemetery on the north-western edge of the Piazza dei Miracoli, the same piazza on which the famous leaning tower stands.

Today, most of the few people who have ever heard of Leonardo probably know of him only through his association with so-called Fibonacci numbers, which were named after him. These are numbers which lie in the sequence that begins 1, 1, 2, 3, 5, …. , and in which each number is the sum of the two immediately preceding it. But Leonardo did not discover these numbers themselves, nor any of their significant properties. His only connection with them is that they arose in a whimsical example which he included in his most significant work merely as an illustration of how certain problems could be solved with the techniques of calculation he wished to explain.

Leonardo’s importance to the intellectual development of Europe stems neither from his association with Fibonacci numbers, nor from any of his original mathematical discoveries, but from his influential works promoting use of the now familiar Hindu-Arabic numerals. The chief of these was a monumental Latin treatise of around six hundred pages – Liber abaci (Book of calculation) – first published in 1202.

By the time of Leonardo, European scholars had already known of Hindu-Arabic numerals for more than a century. However, they had remained little more than an academic curiosity, known only to such scholars. In European practice, numbers were still being recorded with Roman numerals, and arithmetical calculations were not carried out in writing, but with mechanical aids such as calculating tables, abacuses, or – for the simplest calculations – just fingers, by specially trained bookkeepers.

The development of Hindu-Arabic numerals occurred in India during the first millennium AD and had been completed by about the year 700. They came to the notice of the Arabs shortly thereafter, who recognised their advantages and swiftly adopted them as their standard method for representing numbers. European scholars became acquainted with them from about the late 10th century through contact with the Arabs, and translations of some of their mathematical works into Latin.

The chief advantage of the Hindu-Arabic decimal system is the relative simplicity of its procedures for multiplication and division. Roman numerals are poorly adapted for performing these operations, with division being especially cumbersome. It has often been claimed that the only way to perform these operations with Roman numerals is by repeated addition and repeated subtraction, respectively. This is something of an exaggeration, however.

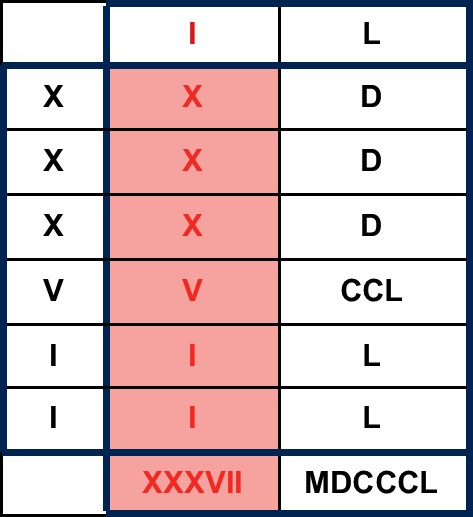
XXXVII x IL = MDCCCL – XXXVII= MDCCCXIII
49
37
______
343
1470
______
1813
Calculation of 49 x 37 using Roman numerals and Hindu-Arabic decimals

In the above diagram, the same pair of numbers, 49 and 37, are multiplied together using both Roman and Hindu-Arabic numerals. One way to perform this calculation with Roman numerals, is to write one factor above the top row and the other to the left of the leftmost column of a table in which the products of the individual components of the numerals are recorded. The number, CCL, in the fourth row and second column of the table, for instance, is the product of the number, V, to the left of that row and the number, L, above that column. The result of the multiplication is obtained by subtracting the sum of the numbers in the first column from the sum of those in the second. Nevertheless, if Leonardo’s contemporaries were aware of any procedures like this, they found them too cumbersome to use in practice, and the mechanical aids mentioned earlier were universally used for all but the very simplest arithmetical calculations.

This had the disadvantage that none of the intermediate steps in a calculation were ever recorded – only the operands and the final result being written down. Thus, checking the calculation required the whole of it to be redone entirely from scratch. On the other hand, after a calculation with Hindu-Arabic decimals has been written down, all the intermediate steps have been recorded, and can be checked at a glance. In Leonardo’s time, when accurate recording and auditing of financial transactions was rapidly becoming more important, this was a huge advantage of written calculations using the Hindu-Arabic system.

Leonardo learnt the details of the Hindu-Arabic system directly from Berbers of North Africa. At the time, Pisa was one of the prominent Italian maritime republics, along with Genoa, Venice and Ancona, and was engaged in extensive trade and commerce with many cities around the Mediterranean coast. Leonardo’s father, Guilielmo, was a Pisan merchant who was appointed a customs official and trade representative in Bugia, on the Barbary coast – now Bejaïa, in Algeria – some time between 1180 and 1185. Shortly after his arrival, he called for his son to join him, and had him receive instruction in the school of accounting there.

It is very likely, though not certain, that Leonardo became fluent in Arabic, but, in any case, his inquisitiveness and intelligence led him to pick up an extensive knowledge of Arabic mathematics, and, owing to his familiarity with business procedures, he, more than any other European before him, was able to recognise and clearly demonstrate the advantages of the Hindu-Arabic system for the routine arithmetical calculations arising in the normal course of doing business.

Leonardo wrote Liber abaci after returning to Pisa, where it was published in 1202. No copies of this first edition of the work are known to have survived, but Leonardo produced an extended and amended second edition in 1228, of which several manuscript copies dating to the 14th or late 13th century are still extant. The book was a masterpiece of exposition – rigorous, comprehensive, and well-organised – of all the known techniques and methods of calculation of Hindu-Arabic arithmetic. Although the treatment could certainly be described as scholarly, it was also accessible to merchants, bankers and other businessmen, who constituted its main intended audience. One of the features of the book which made it attractive to this audience was the inclusion of copious worked examples of the kinds of practical calculations that would be useful for them.

Although Leonardo became famous within his lifetime, history has not recorded the extent to which the revolution he initiated had proceeded at the time of his death. By the end of the 13th century, however, it was well under way. From that time onwards, scuole d’abaco – schools of arithmetic – in which young children were being taught modern arithmetic were springing up all over Italy. At the same time, tracts explaining the new arithmetic proliferated rapidly, to satisfy a burgeoning market for them. Leonardo’s influence on these developments can be traced through the unmistakable dependence of these tracts on his works.

David Wilson